What determines is resistor connections are in series or parallel? Resistor in Series and parallel formula | Calculator class 10

Series and Parallel Resistor

Most circuits have more than one resistor.  If several resistors are connected together and connected to the battery, the current supplied by the battery depends on the equivalent resistance of the circuit.

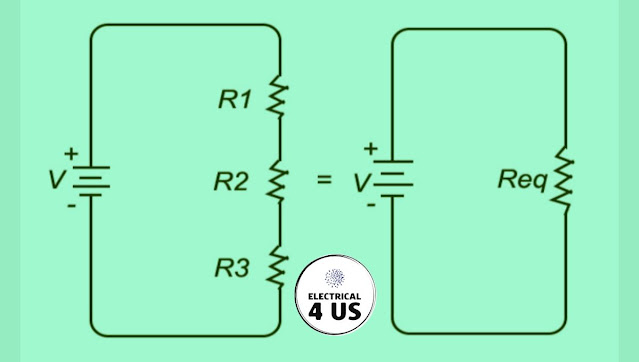
Series Resistor

Resistors are said to be in series whenever current flows through the resistors sequentially.  Consider Figure below, which shows three resistors in series with an applied voltage equal to V(Ab).  Since there is only one path for the flow of charges, the current through each resistor is the same.

Resistor in Series

The equivalent resistance of a set of resistors in a series connection is equal to the algebraic sum of the individual resistors.  As the current through each component is the same, the analogy can be simplified to a uniform resistance, which is simply the sum of the resistances of the individual resistors.  Any number of resistors can be connected in series.  If N resistors are connected in series, then the equivalent resistance is

 Req = R1 + R2 + R3 + ...+Rn

 leq = l1= l2 l3 = in

 leq = l1 + l2 +l3 + ... + In

 Veq = V1 + V2 +V3+....+vn

One consequence of components connected in a series circuit is that if something happens to one component, it affects all other components.  For example, if several lamps are connected in series and one bulb burns out, all the other lamps go dark.

Req= 1/ R1 +1/R2+ 1/R3 = V

Parallel Resistor

Resistor are in parallel when one of ends of all the resistors are connected by a continuous wire of negligible resistance and the other end of all the resistors is also connected to each other through a continuous wire of negligible resistance. The potential drop across each resistor is the same.

Resistor in Parallel

The current through each resistor can be found using Ohm's law I = V/R, where the voltage is constant across each resistor.  Normalizing to any number of N resistors, the equivalent resistance R(eq) of a parallel connection is related to the individual resistances by tra. 

Req = 1 / R1 + 1 / R2 + 1 / R3 + .. + 1 /Rn

 Leq = l1 + l2 +l3 + ... +in

 Veq = V1 = V2 = V3 = Vn

An equivalent resistance has R(eq) which is less than the smallest of the individual resistors.  When resistors are connected in parallel, more current flows through the source than either of them flows separately.